1、我们先有两个函数f(x),g(x)。这两个函数都在x趋向于0时,趋向于0,并且g(x)恒不等于0。

2、高阶无穷小。当x趋向于0时,极限值为0。f(x)为g(x)的高阶无穷小。

3、低阶无穷小。当x趋向于0时,极限值为无穷。f(x)为g(x)的低阶无穷小。
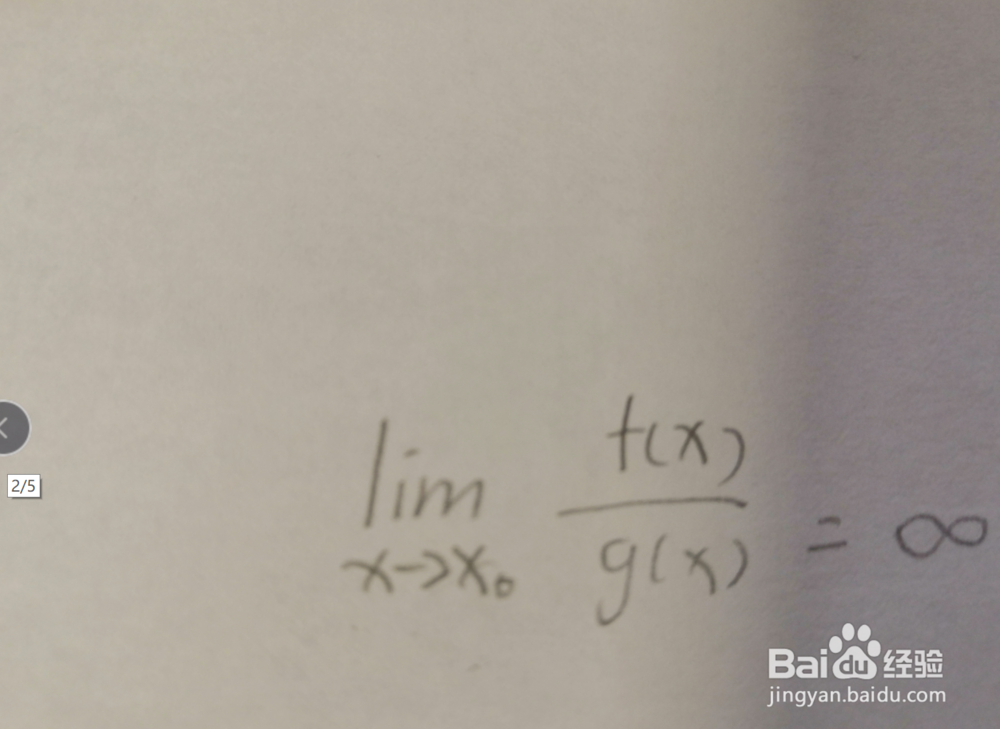
4、同阶无穷小。当x趋向于0时,极限值为一个常数。f(x)为g(x)的同阶无穷小。
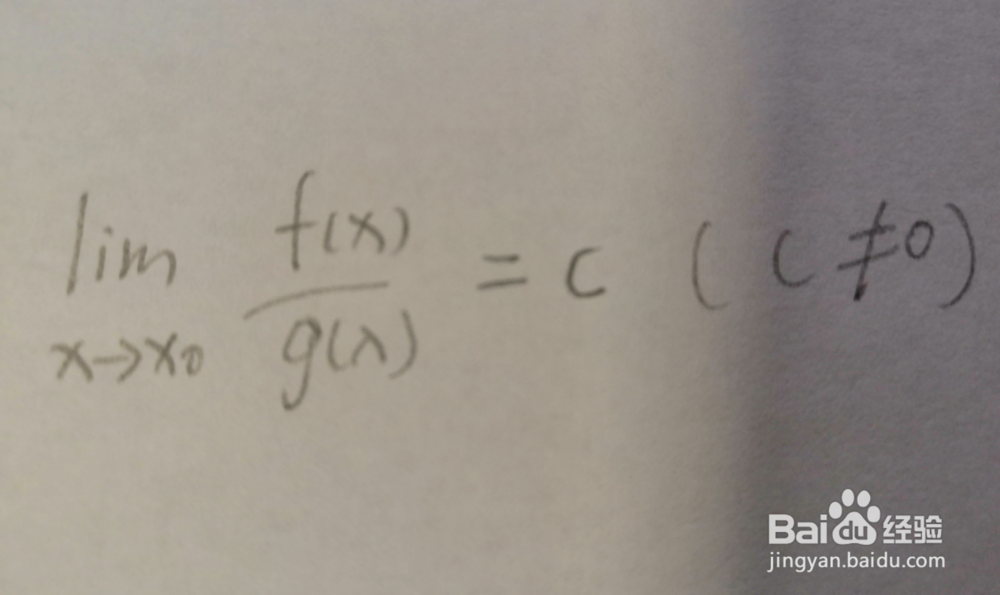
5、等阶无穷小。当x趋向于0时,极限值为1。f(x)为g(x)的等阶阶无穷小。
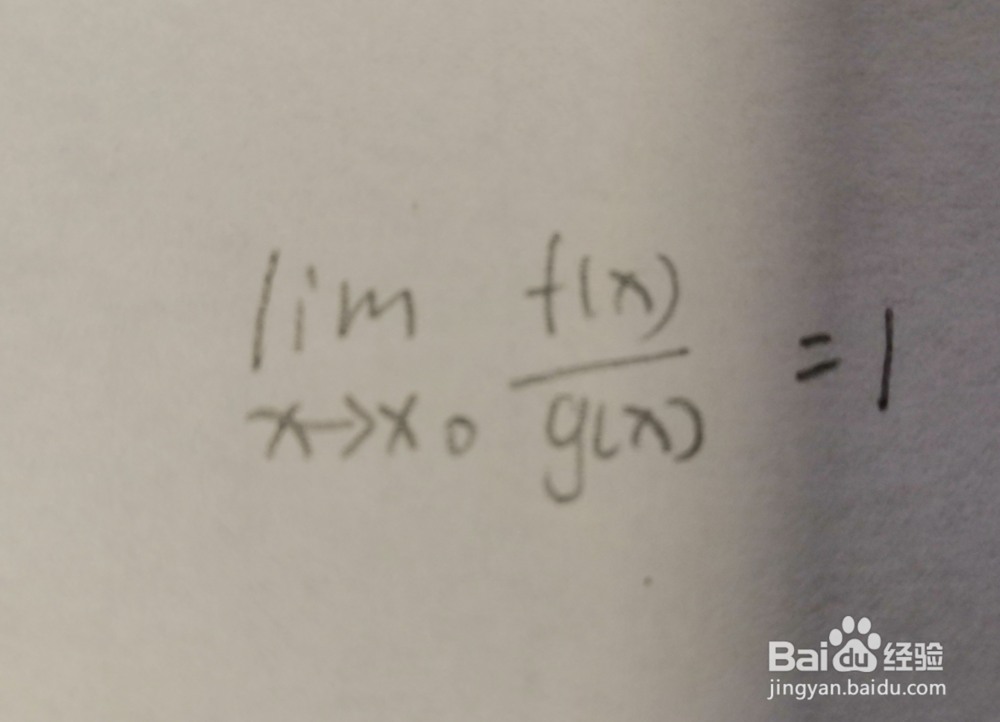
6、一些常用的等价条件是比较重要的,需要我们记住。

1、我们先有两个函数f(x),g(x)。这两个函数都在x趋向于0时,趋向于0,并且g(x)恒不等于0。

2、高阶无穷小。当x趋向于0时,极限值为0。f(x)为g(x)的高阶无穷小。

3、低阶无穷小。当x趋向于0时,极限值为无穷。f(x)为g(x)的低阶无穷小。
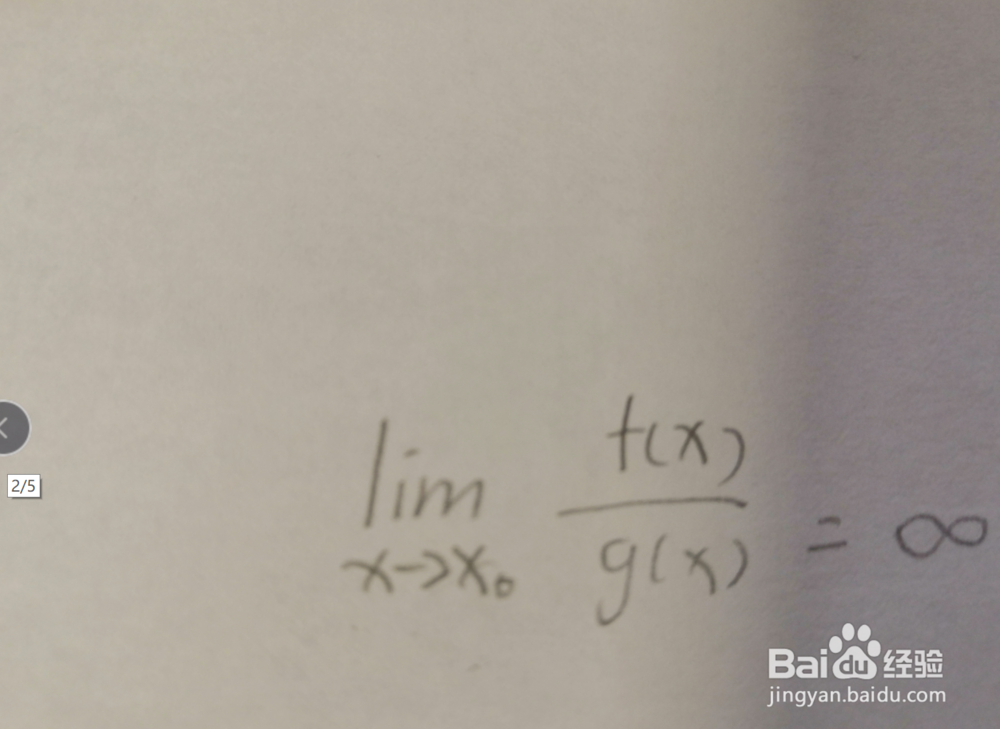
4、同阶无穷小。当x趋向于0时,极限值为一个常数。f(x)为g(x)的同阶无穷小。
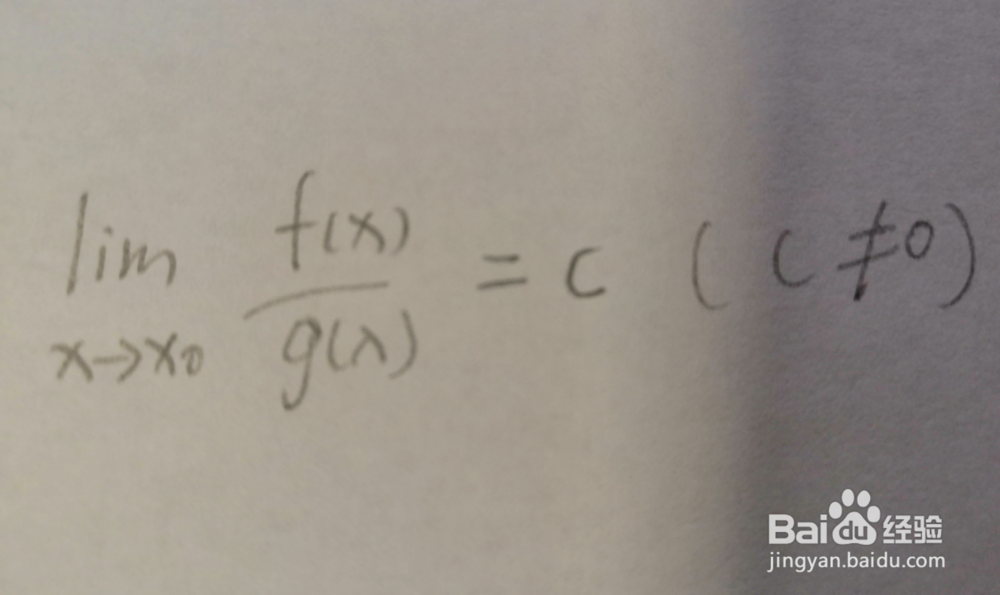
5、等阶无穷小。当x趋向于0时,极限值为1。f(x)为g(x)的等阶阶无穷小。
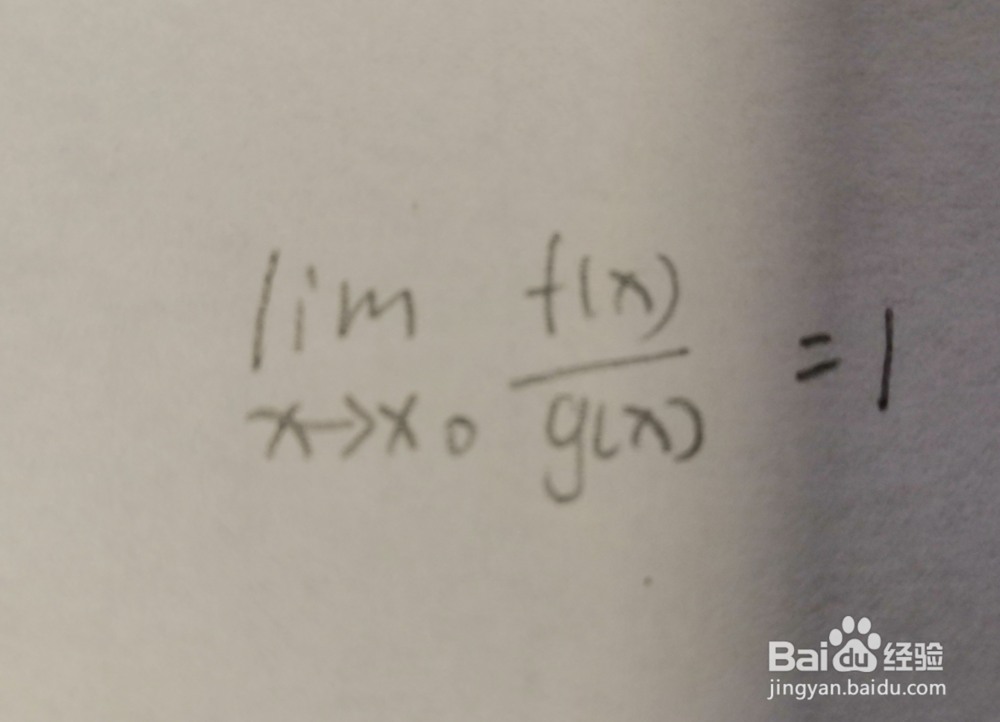
6、一些常用的等价条件是比较重要的,需要我们记住。
