【抽象代数】用Mathematica判定代数整数

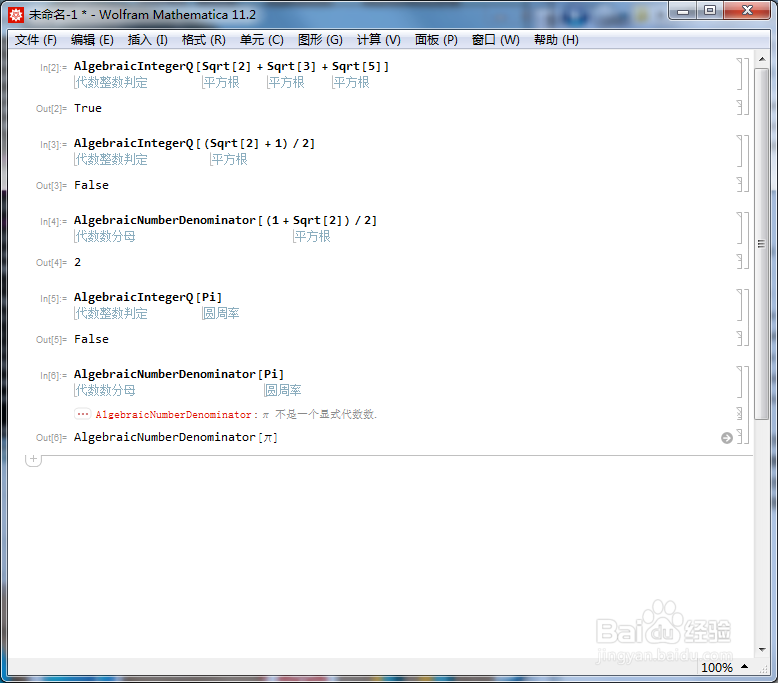
1、判断Sqrt[2] + Sqrt[3] 是不是代数整数的方法是：AlgebraicIntegerQ[Sqrt[2] + Sqrt[3] ]返回结果是True，则表示它是代数整数。

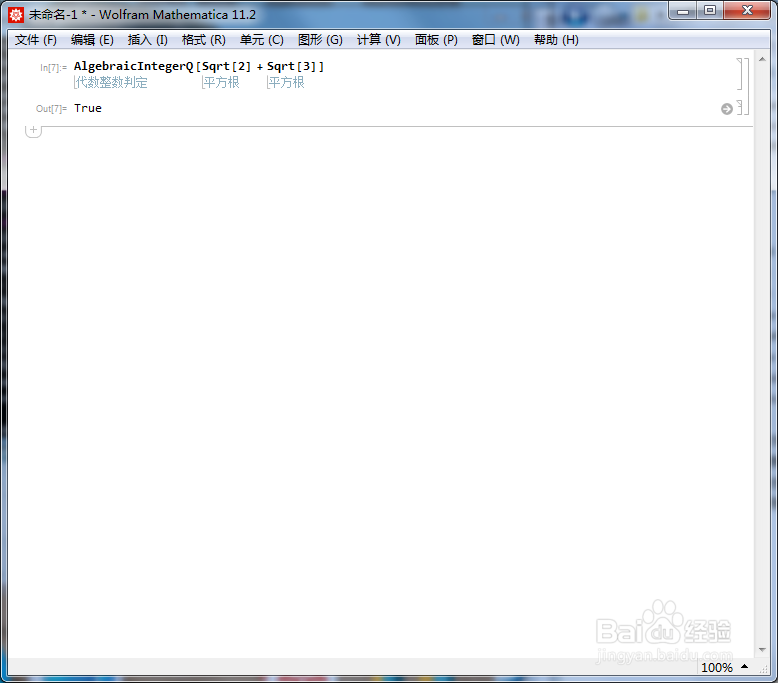
2、Sqrt[2] + Sqrt[3] + Sqrt[5]也是代数整数。AlgebraicIntegerQ[Sqrt[2] + Sqrt[3] + Sqrt[5]]

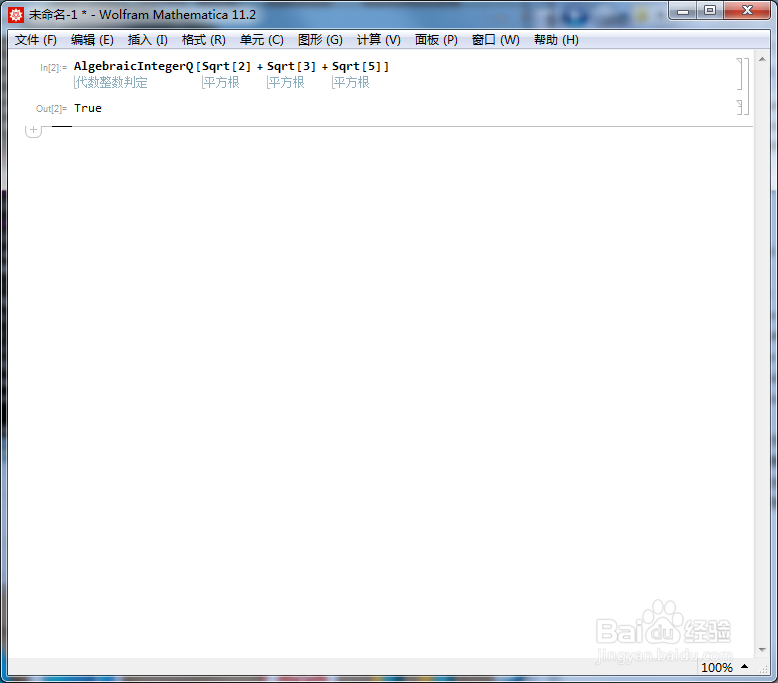
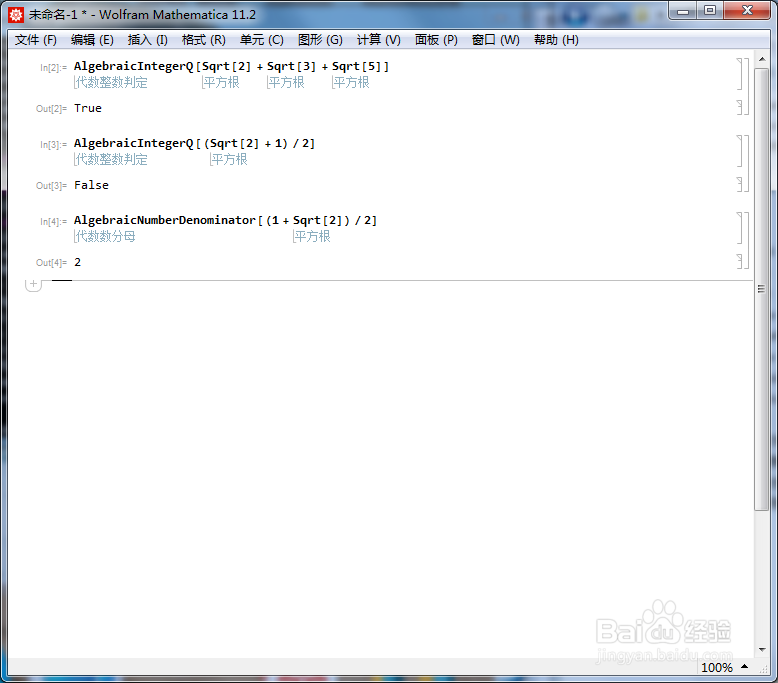
3、(Sqrt[2] + 1)/2不是代数整数，所以返回的结果是False。AlgebraicIntegerQ[(Sqrt[2] + 1)/2]

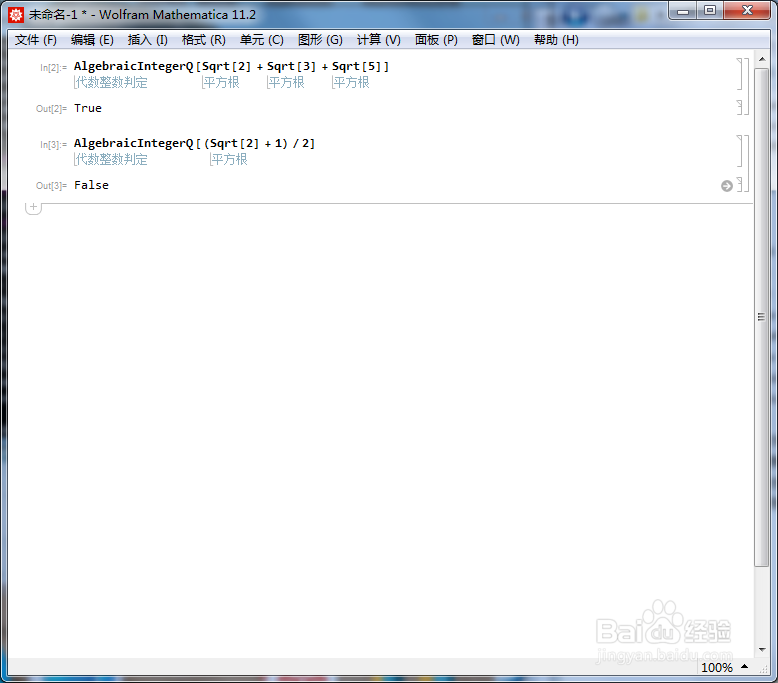
4、(Sqrt[2] + 1)/2乘上一个正整数n，使之变成一个代数整数，n最小是多少？用下面的代码可以求出来：AlgebraicNumberDenominator[(1 + Sqrt[2])/2]

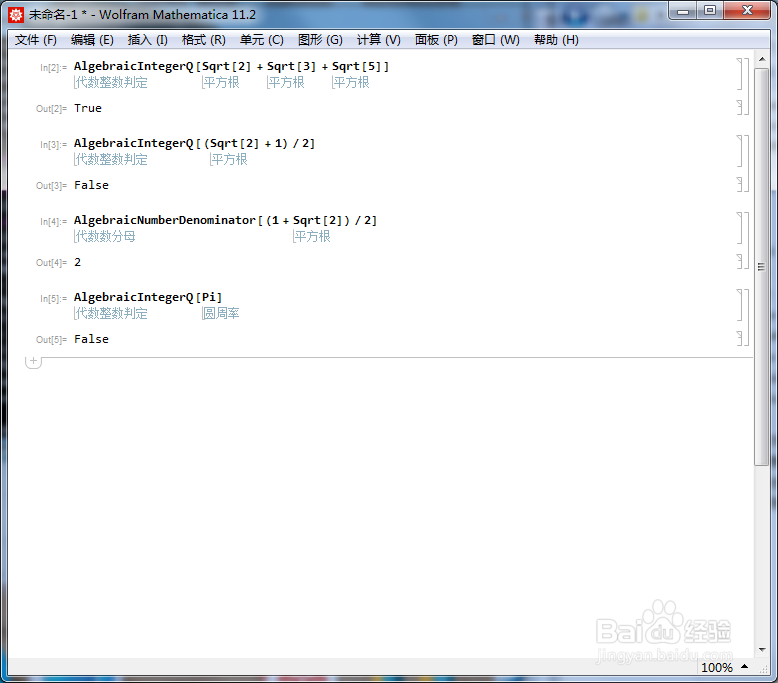
5、圆周率π不是代数整数：AlgebraicIntegerQ[Pi]

6、看看π要乘上一个多大的正整数，才能变成代数整数：AlgebraicNumberDenominator[Pi]结果报错，其根源是，π不是代数数。