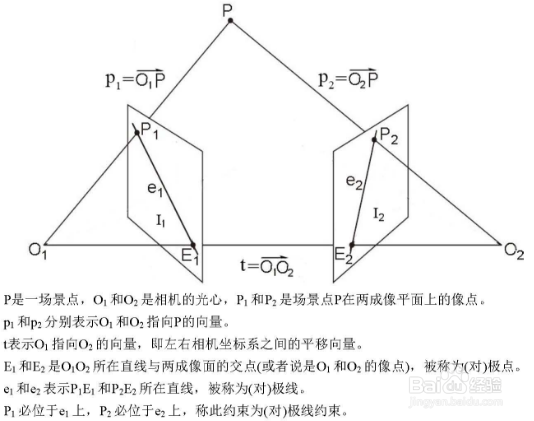
1、对极线约束:空间点P,O1和O2为相机光心,P1和P2为点P的像点,p1和p2为O1和O2指向P的向量;t为O1指向O2的向量,即左右相机坐标系之间的平移向量;E1和E2为O1O2所在直线与两成像面的交点,称为对极点;e1和e2表示P1E1和P2E2所在直线,被称为对极线;P1必位于e1上,P2必位于e2上,称此约束为对极线约束;
2、本征矩阵的定义:①p1和t是以左相机坐标系为基准,p2是以右相机坐标系为标准;当p2是以右相机坐标系为标准后,在左相机坐标系中对应的p2为R-1p2。其中,R是左右相机之间的旋转矩阵(右相对左的)。②因为p1,p2和t共面,所以三者的混合积,即;由于旋转矩阵R是正交矩阵,所以,所以;称矩阵E=RS为本征矩阵:其秩为2;只与两相机坐标系之间的位姿关系相关;【注】:p1是左坐标系中向量或坐标,p2是右坐标系中向量或坐标;R和t是右相机坐标系相对于左相机坐标系的旋转矩阵和平移向量;

3、基础矩阵的定义:设p1和p2对应的像素坐标分别为q1和q2,两相机的投影矩阵分别为M1和M2,则称矩阵为基本矩阵;其秩为2;与两相机坐标系之间的位姿关系和两相机之间的投影矩阵有关;【注】:q1是左视图中的像素坐标;q2是右视图中的像素坐标;

4、本征矩阵的数学变换:由于不能上传公式,故通过图像的方式来描述;由对极几何约束条件,本征矩阵的推导过程如下图所示;本征矩阵的性质:①其秩为2;②只与两相机坐标系之间的位姿关系相关;


5、基础矩阵的数学变换:结左佯抵盗合程序的几何关系,有如下公式:像平面上的一点可以看作:• (u,v) 2D film poi荏鱿胫协nt(局限于像平面上来考虑)• (u,v,f) 3D point on film plane(相机坐标系中来考虑)• k(u,v,f) viewing ray into the scene(透过像点和原点射线上点的像,相机坐标系中来考虑)• k(X, Y, Z) ray through point P in the scene(在世界坐标系中来考虑)几何的观点:左像平面上的一点乘以本质矩阵,结果为一条直线,该直线就是的极线,且过在右像平面上的对应点。基础矩阵的性质:①其秩为2;②与两相机坐标系之间的位姿关系和两相机之间的投影矩阵有关;


6、单应性矩阵H:homography matrix通过四个坐标系之间的变换,单应性矩阵H来自不同角度的拍摄;单应矩阵的定义与R、t、平面参数相关,单应矩阵为3*3的矩阵,自由度为8,求解的思路和E、F相似。求解:可用一组不共线但共面的4个匹配点来计算矩阵H。

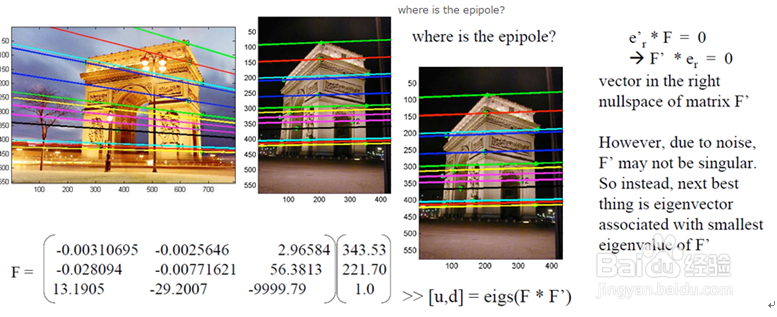
7、示例: