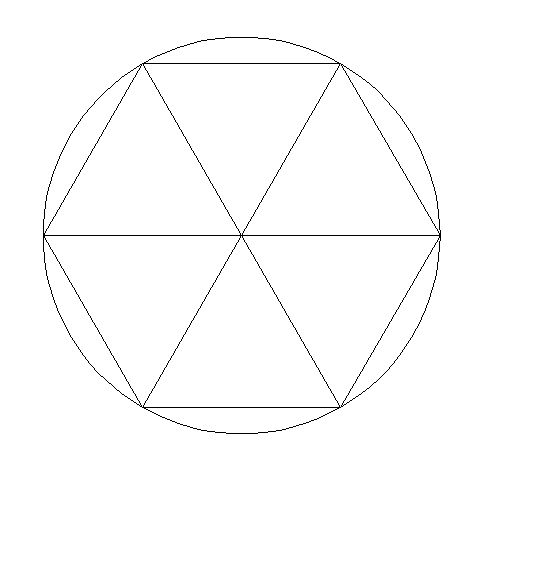
圆心到正n边形所有顶点的连线都是半径,长度为R.
这些连线将正n边形分成了n个全等的等腰三角形.这样,每个三角形的顶角为2π/n,腰长为R,
设正多边形边长为x,过圆心做等腰三角形底边上的垂线,在分成的一个直角三角形里用三角函数:
sin((2π/n)/2)=(x/2)/R
x=2Rsin(π/n).
设边心距为y,y=Rcos(π/n)
每个等腰三角形的面积=边长×边心距/2
=Rcos(π/n)*2Rsin(π/n)/2
=R*Rsin(π/n)cos(π/n)
=R*Rsin(2π/n)/2
正多边形的面积
=R*Rsin(2π/n)/2 × n
=nR*Rsin(2π/n)/2
扩展资料
主要思想是用“相似三角形”来做。
内、外一条边,分别连接边的端点与圆心,得到一大一小两个等腰三角形,这两个三角形相似,证明略;边长a,b之比即为两等腰三角形底边上的高之比。大三角形的高为圆半径r。小三角形的高为r*cos(360°/2n)。(因为是正n边形)故b=a/cos(360°/2n).
周长L=2nr*sin(180/n)°,绝对不要写成180°/N,而是(180/n)°,粗心大意的人往往第一步就写成XX°/n,后面不用看了,一分拿不到,白算半天。
面积S=n/2*R^2*sin(180/n)°*cos(180/n)°。
sinA*cosA=1/2sin(2A),所以还可以化简,S=n/4*R^2*sin(360/n)°