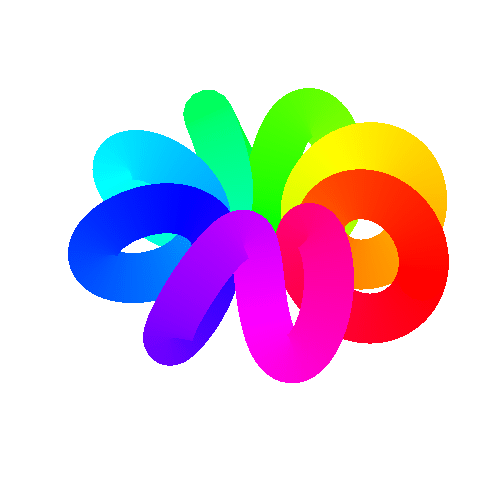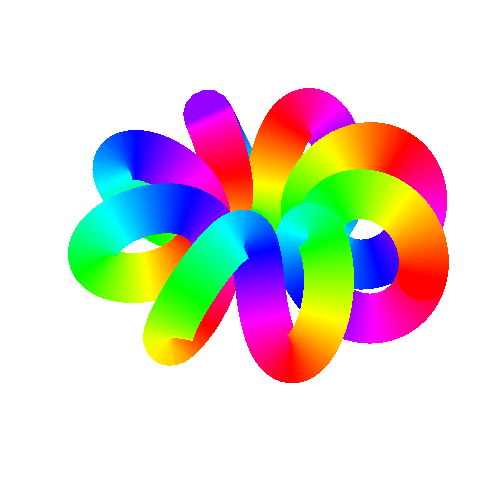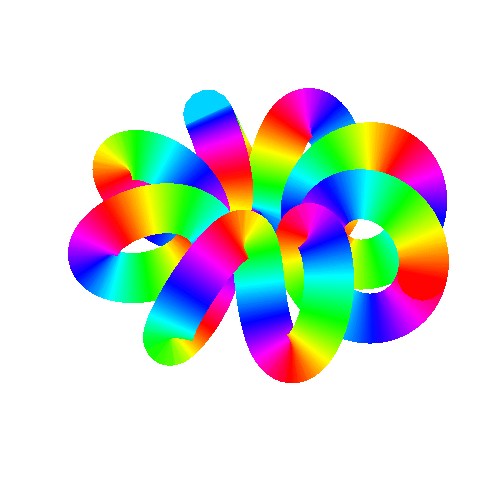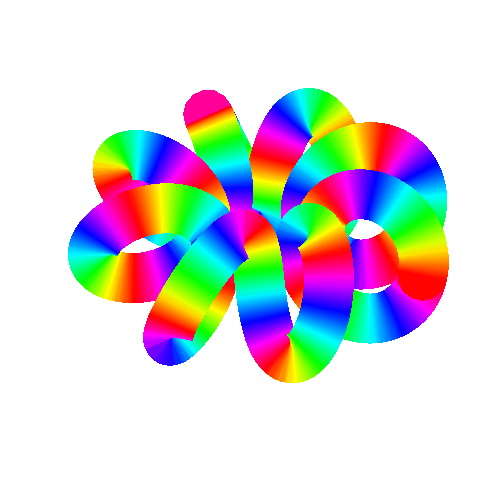1、 先来吸睛——一个半透明的绿贝壳:
ParametricPlot3D[{1.16^v Cos[v] (1 + Cos[u]), -1.16^v Sin[v] (1 + Cos[u]), -2 1.16^v (1 + Sin[u])}, {u, 0, 2 Pi}, {v, -15, 6},
Mesh -> None, PlotStyle -> {Opacity[0.6], Green}, PlotRange -> All,
PlotPoints -> 25, Boxed -> False, Axes -> False]


2、 另一条参数化的曲面:
ParametricPlot3D[{Cos[u], Sin[u] + Cos[v], Sin[v]}, {u, 0, 2 \[Pi]}, {v, -\[Pi], \[Pi]}, Mesh -> None, Axes -> False,
Boxed -> False, PlotStyle -> {Opacity[1], Green}】

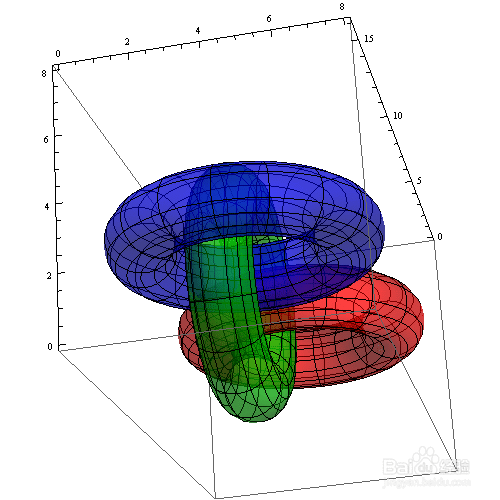
3、 绘制两个套在一起的圆环,两个圆环红绿相间:
ParametricPlot3D[{{4 + (3 + Cos[v]) Sin[u], 4 + (3 + Cos[v]) Cos[u],
4 + Sin[v]}, {8 + (3 + Cos[v]) Cos[u], 3 + Sin[v],
4 + (3 + Cos[v]) Sin[u]}}, {u, 0, 2 Pi}, {v, 0, 2 Pi},
PlotStyle -> {{Opacity[0.6], Red}, {Opacity[0.6】, Green}},
Mesh -> None, Axes -> False, Boxed -> False】
注意透明度是分别设置的!

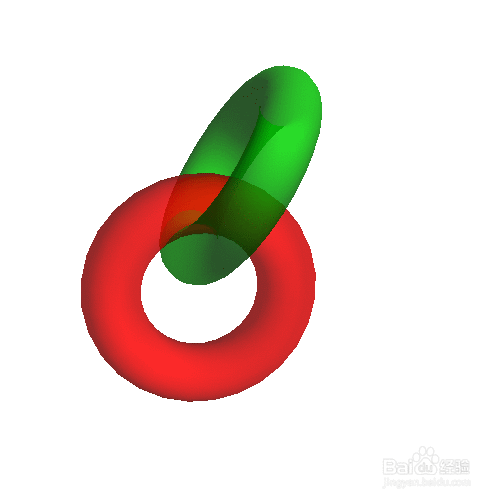

4、 三个圆环套在一起,用不同的颜色加以区分:
ParametricPlot3D[{{4 + (3 + Cos[v]) Sin[u], 4 + (3 + Cos[v]) Cos[u],
4 + Sin[v]}, {8 + (3 + Cos[v]) Cos[u], 3 + Sin[v],
4 + (3 + Cos[v]) Sin[u]}, {12 + (3 + Cos[v]) Sin[u],
4 + (3 + Cos[v]) Cos[u], 4 + Sin[v]}}, {u, 0, 2 Pi}, {v, 0, 2 Pi},
PlotStyle -> {{Opacity[0.5], Red}, {Opacity[0.5],
Green}, {Opacity[0.5], Blue}}]
读者可以自己思考一下,如何画出三个互相缠绕的圆环?


5、 绘制一个不透明的蓝色球体,表面有均匀的波浪条纹,还有白色的高光反射:
ParametricPlot3D[{Sin[u] Sin[v] + 0.05 Cos[20 v],
Cos[u] Sin[v] + 0.05 Cos[20 u],
Cos[v]}, {u, -\[Pi], \[Pi]}, {v, -\[Pi], \[Pi]}, MaxRecursion -> 4,
PlotStyle -> {Blue, Specularity[White, 10]}, Axes -> None,
Boxed -> False, Mesh -> None]
高光反射,用Specularity控制。

6、 画贝壳的时候,在变化区域较快的区域,增加网格线的密度:
ParametricPlot3D[{1.16^v Cos[v/2] (1 + Cos[u]), -1.16^v Sin[
v/2] (1 + Cos[u]), -2 1.16^v (1 + Sin[u])}, {u, 0,
2.6 Pi}, {v, -15, 6}, Mesh -> All, PlotRange -> All, Boxed -> False,
Axes -> False, PlotStyle -> {Opacity[0.9], Pink}】


7、 绘制三维空间的曲线——单参数是曲线,双参数是曲面:
ParametricPlot3D[{Cos[2 u], Sin[2 u], Sqrt[u] + Sin[5 u]/5}, {u, 0,
4 Pi}, Mesh -> All, PlotStyle -> {Pink}


8、 Mathematica会自动选择画图的区域范围,以下面的“长号”为例:
ParametricPlot3D[{v Cos[u], v Sin[u], 1/Abs[v Exp[I u]]}, {u, 0,
2 Pi}, {v, 0, 1}, PlotStyle -> RGBColor[0, 0.7, 0.3],
Boxed -> False, Axes -> False】
这里,坐标隐藏了。你可以把“, Axes -> False”删掉,可以看到坐标系。

9、 当曲面不连续的时候,Mathematica会自动忽略掉无法显示的部分:
ParametricPlot3D[{u Cos[v], u Sin[v], Im[(u Exp[I v]^5)^(1/5)]}, {u,
0, 2}, {v, 0, 2 Pi}, Mesh -> None, ExclusionsStyle -》 {None, Red}]

10、 弹簧绕成一个圈会是什么模样呢?
ParametricPlot3D[
Evaluate[Table[{(2 + Cos[8 u + i】) Cos[u], (2 + Cos[8 u + i]) Sin[u],
Sin[8 u + i]}, {i, {0, Pi}}]], {u, 0, 2 Pi}】

11、 给它起个名字叫“弹簧线圈”:
ParametricPlot3D[{(2 + Cos[8 u]) Cos[u], (2 + Cos[8 u]) Sin[u],
Sin[8 u]}, {u, 0, 2 Pi}, AxesLabel -> {x, y}, PlotLabel -> “弹簧线圈”]

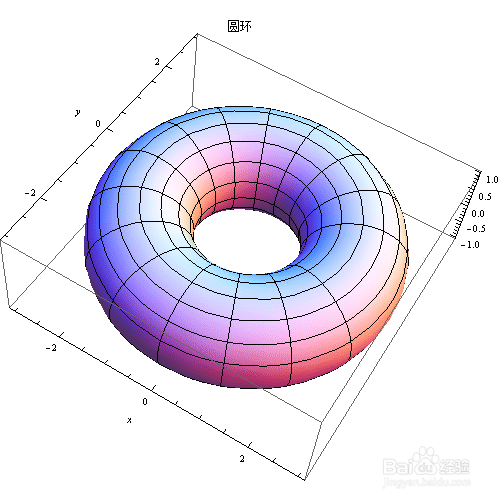
12、 有两种方法可以画一个圆环。
第一种方法是用RevolutionPlot3D旋转一个圆得到圆环,这里先忽略;
第二种方法:
ParametricPlot3D[{(2 + Cos[v]) Cos[u], (2 + Cos[v]) Sin[u],
Sin[v]}, {u, 0, 2 Pi}, {v, 0, 2 Pi}, AxesLabel -> {x, y},
PlotLabel -> “圆环”]
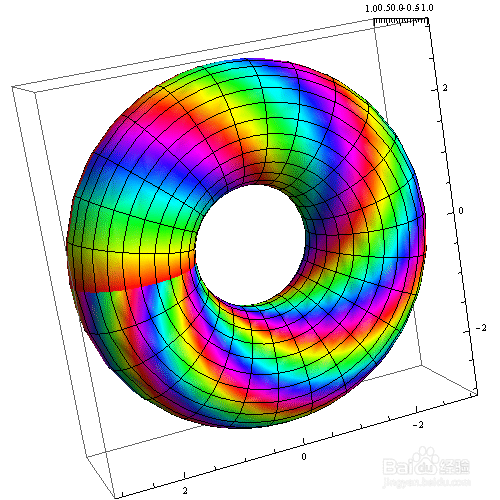
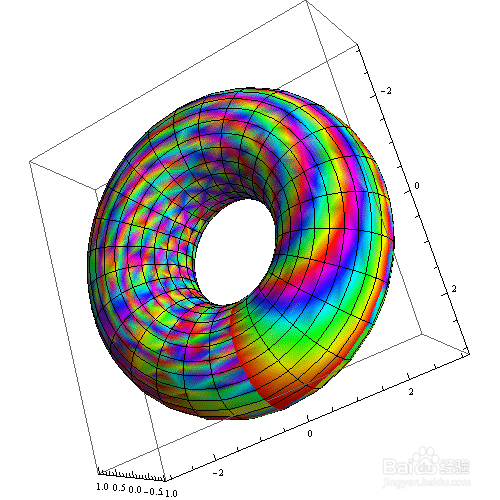
13、 用ColorFunction把“线圈”和“圆环”画成彩色:
ParametricPlot3D[{(2 + Cos[v]) Cos[u], (2 + Cos[v]) Sin[u],
Sin[v]}, {u, 0, 2 Pi}, {v, 0, 2 Pi}, Mesh -> 25,
ColorFunction -> Function[{x, y, z, u, v}, Hue[5 u v/(2 Pi)]],
ColorFunctionScaling -> False]
和
ParametricPlot3D[{(2 + Cos[8 u]) Cos[u], (2 + Cos[8 u]) Sin[u],
Sin[8 u]}, {u, 0, 2 Pi}, PlotStyle -> Thick,
ColorFunction -> Function[{x, y, z, u}, Hue[5 u/(2 Pi)]],
ColorFunctionScaling -> False]

14、 上面的动态图片如下。


15、 先到这里吧!