1、从最简单的开始。如果读者对Integrate比较了解,可直接看第四步。
首先,我们使用Integrate对Exp[-(x+y)]计算二重积分。我们看到,其在整个R^2平面上积分的话是不收敛的。如果指定x,y>0则积分收敛到1.

2、为了演示方便,增加可视化方法介绍。
使用Plot3D函数对该函数进行可视化。增加参数PlotRange->Full表示显示完整不截取。

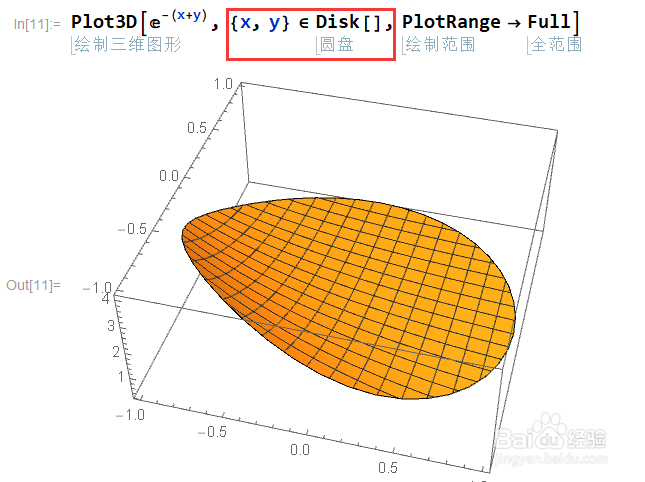
3、在绘图时,可以使用如图方式{x,y}∈Disk[]将坐标限制在单位圆内。
此外,还可以使用RegionFunction限制复杂的显示效果。
4、在积分Integrate中,使用{x,y}∈Disk[]将坐标限制在单位圆内。
对于复杂范围,可以将被积函数乘以Boole函数。Boole函数会判断其中的表达式,返回1或0。
使用N将解析结果化成数值结果,可见如图两种方式结果相同。


5、如果直接对Boole函数绘图,就是高低两层图像。
如果直接对Boole函数积分,就是面积。

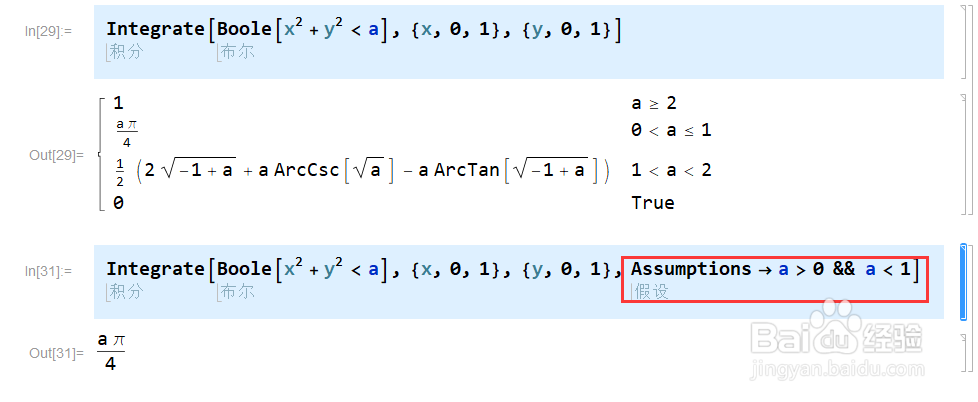
6、Integrate是符号积分,支持不定参数。
如图,Mathematica会自动分类讨论a>=2/0<a<=1/1<a<2和其它。
如果不需要那么多讨论和计算,使用Assumptions进行假设。
语法为:Assumptions->和参数有关逻辑表达式
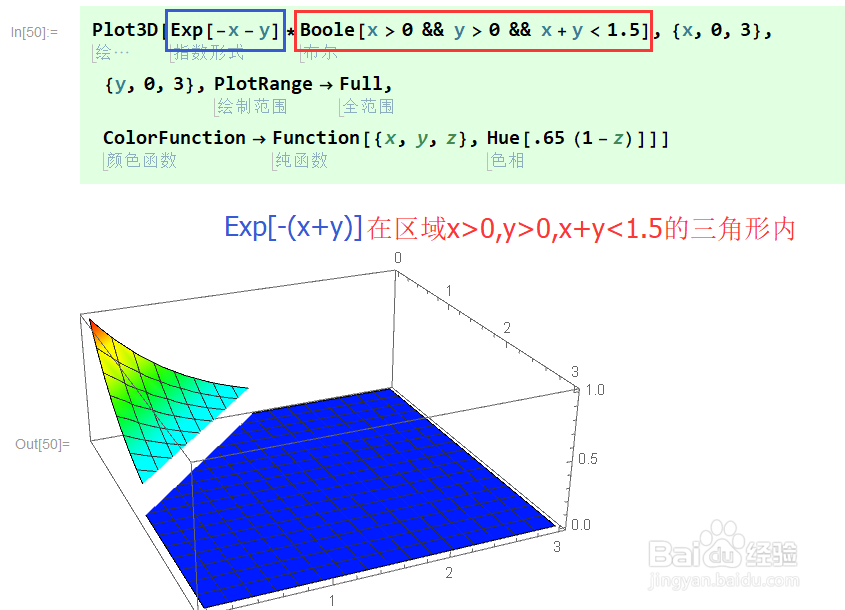
7、如图,是一个概率论习题中的具体案例。计算Exp[-(x+y)]在一个三角形区域内的积分。以及参数等于1.5时的可视化。