1、S.D dependent var是被解释变量Y的标准差,简称SD。
TSS:Total sum of squares,即原始数据和均值之差的平方和。
TSS与SD存在下列关系:
TSS=SD^2*(N-1) ;
2、回归平方和: ESS (explained sum of squares)即预测数据与原始数据均值之差的平方和,这部分差异是回归可解释的部分。
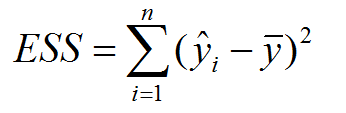
残差平方和 RSS (residual sum of squares),也称剩余平方和。
该统计参数计算的是拟合数据和原始数据对应点的误差的平方和。

总平方和TSS (Total Sum of Squares) 即原始数据和均值之差的平方和,公式如下

三者之间的关系是TSS=RSS+ESS
由此,可以得到:ESS=TSS-RSS=SD^2*(N-1)-RSS
扩展资料:
1、S.D dependent var是被解释变量Y的标准差。标准差(Standard Deviation),是离均差平方的算术平均数的平方根,是方差的算术平方根。S.D dependent var反映被解释变量Y的离散程度。
2、TSS(Total sum of squares)原始数据和均值之差的平方和。与SD存在下列关系:
TSS=SD^2*(N-1) ;
3、决定系数是因变量Y的变异中有多少百分比,可由控制的自变量X来解释. 在Y的总平方和中,由X引起的平方和所占的比例。
表达式:R平方=ESS/TSS=1-RSS/TSS