1、首先给出椭圆的方程式：椭圆 = x^2/a^2 + y^2/b^2 - 1;
2、考虑经过椭圆中心点且斜率为k的直线，与椭圆的交点：Solve[{椭圆 == 0, y == k x}, {x, y}]
3、原则上，上述两个解的任意一个，都可以视为椭圆的参数方程。但是注意，斜率k的取值范围是-∞到+∞，螽啸镥释相当于k=tan(t)的t从-π/2到+π/2。我们来作图：With[{a = 5, b = 3},ParametricPlot[{(a b)/Sqrt[b^2 + a^2 Tan[t]^2], (a b Tan[t])/Sqrt[ b^2 + a^2 Tan[t]^2]}, {t, -Pi/2, Pi/2}]]为a和b分别赋值为5和3，但是图像显示，参数方程作图并不完整。
4、另辟他途。我们考虑经过椭圆左顶点，且斜率为k的直线，与椭圆的交点：Solve[{椭圆 == 0, y == k (x + a)}, {x, y}]二者有两个交点，一个是椭圆左顶点，另一个就是椭圆的参数方程。
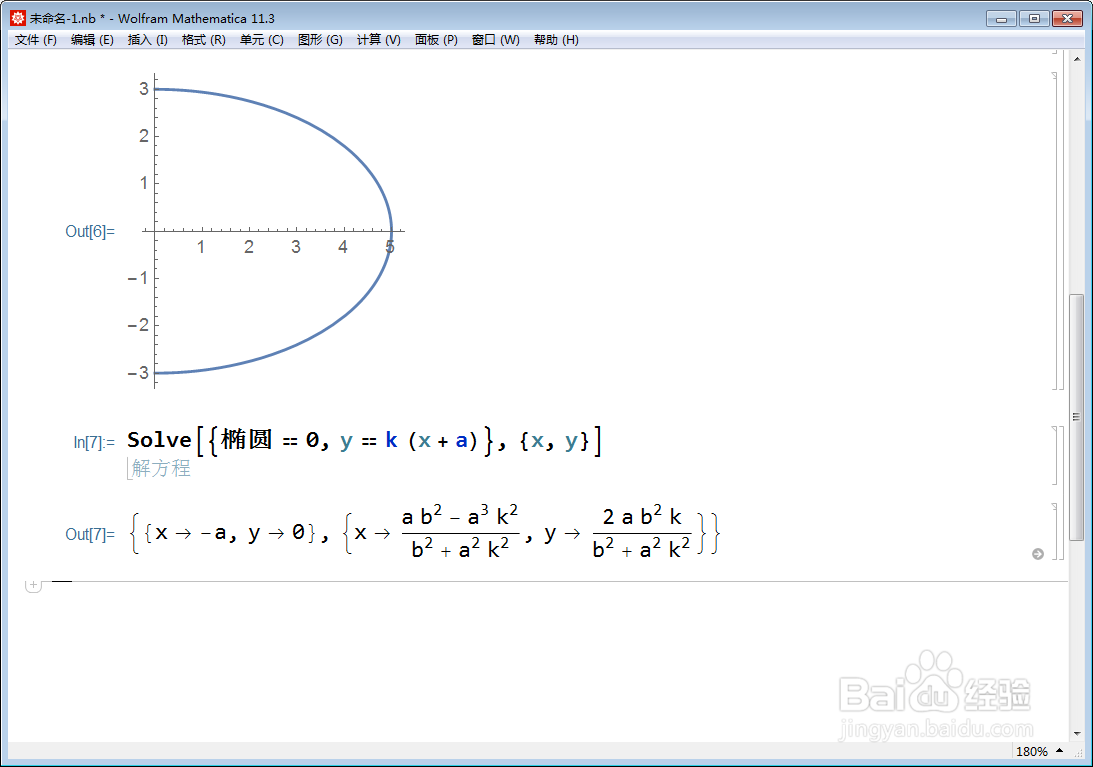
5、我们聪艄料姹再次做图：With[{a = 5, b = 3},ParametricPlot[{(a b^2 - a^3 Tan[t]^2)/(b^2 + a^2 Tan[t]^2), ( 2 a 芟鲠阻缒b^2 Tan[t])/(b^2 + a^2 Tan[t]^2)}, {t, -Pi/2, Pi/2}]]图像完整，说明这个参数方程是对的。
