定义：正棱锥是指底面是正多边形，且从顶点到底面的垂线足是这个正多边形的中心的棱锥，其中，当底面为三角形时，该三角形为等边三角形，只有等边三角形才有中心,等边三角形的重心、外心、垂心、内心重合,称为中心。正棱锥(正多棱锥)的底面是正多边形，侧面全是等腰三角形。
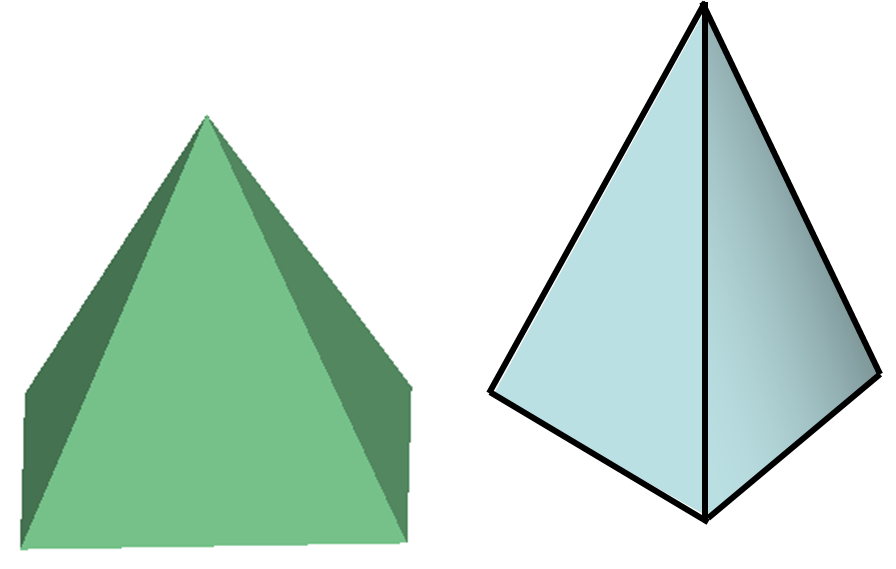
正棱锥性质：
正棱锥的各条侧棱相等。
正棱锥的侧面都是全等的等腰三角形。
正棱锥的对角面都是等腰三角形。
正棱锥的高、侧棱和侧棱在底面内的射影所组成的三角形，都是全等的直角三角形。
正棱锥的高、斜高和斜高在底面内的射影所组成的三角形，都是全等的直角三角形。
正棱锥的斜高都相等。
正棱锥的侧面和底面所成的二面角都相等。
正棱锥的侧棱和底面的交角都相等。
正棱锥的侧面积等于它的底面周长和斜高乘积的一半。
以上内容参考：百度百科——正棱锥