1、函数y=2x^3+4x^2+x为幂函数的四则运算,自变量x可以取全体实数。

2、函数y=2x^3+4x^2+x的单调性解析和单调区间计算。

3、函数的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时,函数值f(x)也随着增大(或减小),则称该函数为在该区间上具有单调性。
4、解析函数y=2x^3+4x^2+x的凸凹性,并计算其凸凹区间。

5、几何的直观解释:如果一个函数f(x)在某个区间I上有f'&拭貉强跳#39;(x)(即二阶导数)>0恒成立,那么在区间I上f(x)的图像上的任意两点连出的一条线段,唁昼囫缍这两点之间的函数图像都在该线段的下方,反之在该线段的上方。
6、二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数y'=f'(x)仍收墩芬蓥然是x的函数,则y'=f'(x)的导数叫作函数y=f(x)的二阶导数。
7、函数y=2x^3+4x^2+x的极限计算。

8、设函数f(x)在x0处的某一去心邻域内有定义,若存在常数A,对于任意ε>0,总存在正数δ,使得当|x-xo|<δ时,|f(x)-A|<ε成立,那么称A是函数f(x)在x0处的极限。
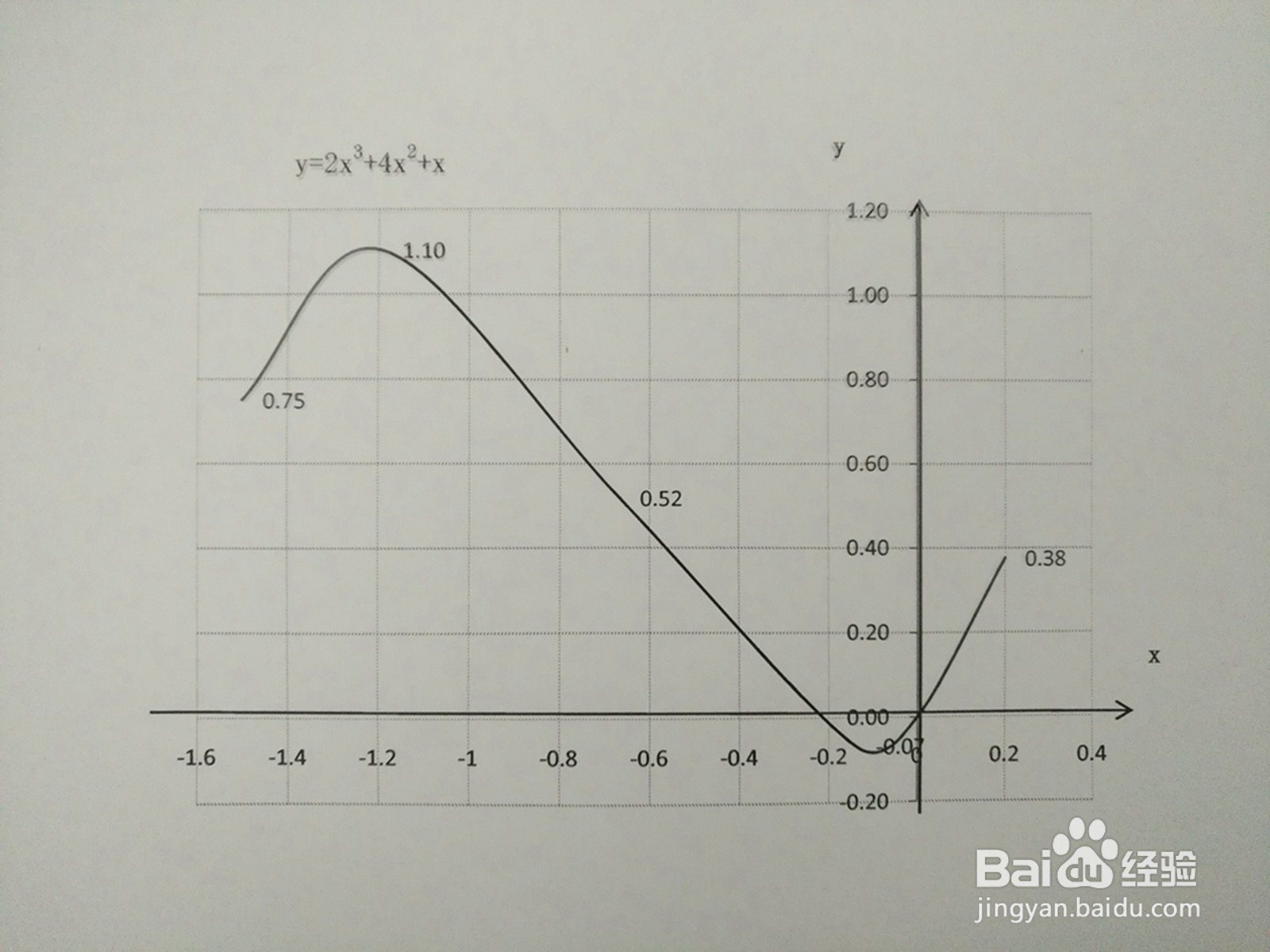
9、函数y=2x^3+4x^2+x上的部分点的五点图。

10、综合函数y=2x^3+4x^2+x的定义域、单调性和凸凹性,函数的示意图如下。