1、首先要知道定义,定义十分重要，由于有些公式无法显示，因此定义在下面图片中。
2、其次根据所给题目，利用定义解题：如下图，要根据数列极限定义证明该极限，因此就需要用到正确的解题方法。
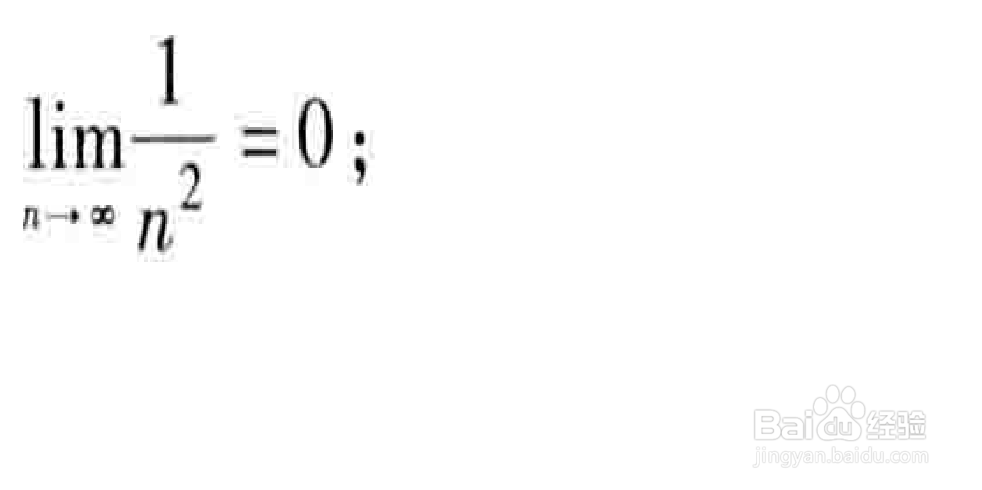
3、证:因为要使|(n^2\1)-0|=猾诮沓靥(n^2\1)<ε,所以只要n>√ε\1,所以对于任意ε>0(不妨设e<I),取N=【√ε\1】，则当n>N时，有|(n^2\1)-0|<ε，所以以上极限成立。
如何根据定义求数列极限
时间：2024-10-15 09:29:281、首先要知道定义,定义十分重要，由于有些公式无法显示，因此定义在下面图片中。
2、其次根据所给题目，利用定义解题：如下图，要根据数列极限定义证明该极限，因此就需要用到正确的解题方法。
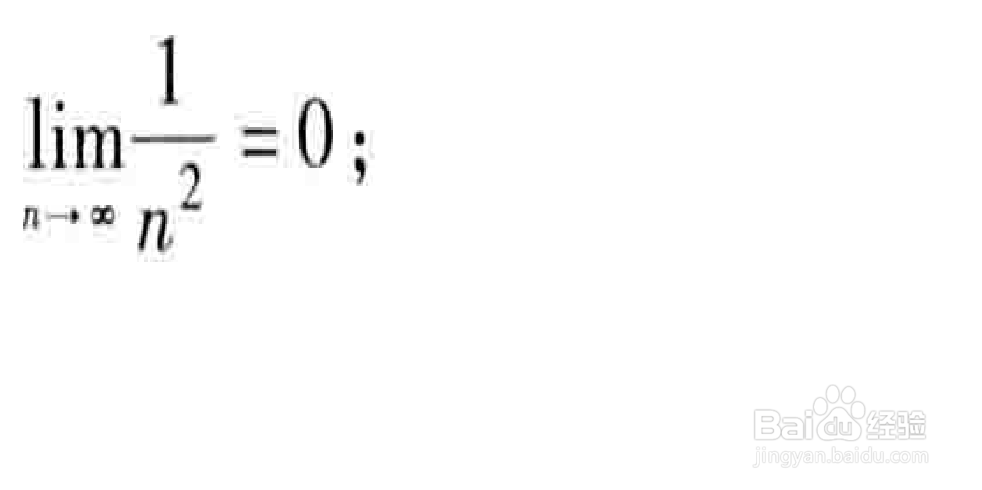
3、证:因为要使|(n^2\1)-0|=猾诮沓靥(n^2\1)<ε,所以只要n>√ε\1,所以对于任意ε>0(不妨设e<I),取N=【√ε\1】，则当n>N时，有|(n^2\1)-0|<ε，所以以上极限成立。