回转半径是指物体微分质量假设的集中点到转动轴间的距离,它的大小等于转动惯量除总质量后再开平方。
比如300*400的柱子:
I=bh^3/12=400*300^3/12
A=400*300
最小回转半径=根号下(I/A)=150√3
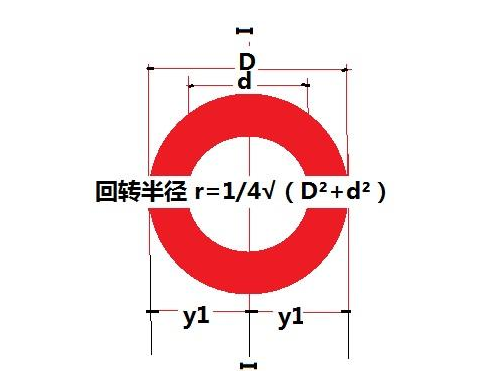
扩展资料:
物体对于一个直轴的回转半径,是与对于此直轴的转动惯量和物体的质量有关。
物理上认为,刚体按一定规律分布的质量,在转动中等效于集中在某一点上的一个质点的质量,假设此点离某轴线的垂距为k,刚体对该轴线的转动惯量与该等效质点对此同一轴线的转动惯量相等,即I=mk^2,则k称为该刚体对该轴线的回转半径。
回转半径的大小与截面的形心轴有关。最小回转半径一般指非对称截面中(如不等边角钢),对两个形心轴的回转半径中的较小者。这在计算构件的长细比时,如构件的平面内和平面外计算长度相等时,它的长细比就要用最小回转半径计算。
结论
1、回转半径仅与截面所在垂直于计算轴的轴的高度有关,也就是仅与截面在垂直于计算轴的方向上的展开程度有关,
2、回转半径与构成截面的板件的厚度和宽度几乎没有什么关系。
3、长方形截面为0.3,中间加一块板变为0.2,比原来降低0.1,是因为惯性矩没有什么变化,但是面积有较大的增加,将中间板移到端部,则变成是0.3,比原来升高0.1,是因为惯性矩有较大的增加,将T形截面的另一端再加上一块板件,则变成0.4,又在原来的基础上升高0.1,这只是一个近似的规律,并且有一定的实用条件,但是对于通常所见的截面一般都能满足以上规律。
物体对于一支直轴的回转半径,是与对于此直轴的转动惯量和物体的质量有关。
参考资料来源:百度百科-回转半径