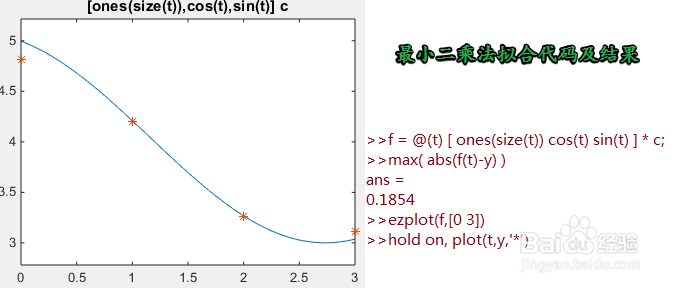
1、 当关系式是基函数的线性组合,并且参数是系数时,其优化是线性最小二乘问题,并且可以使用反斜杠来解决。 例如


2、进一步可以使用匿名函数(使用线性代数快捷方式)来转换成自变量的可调用函数:
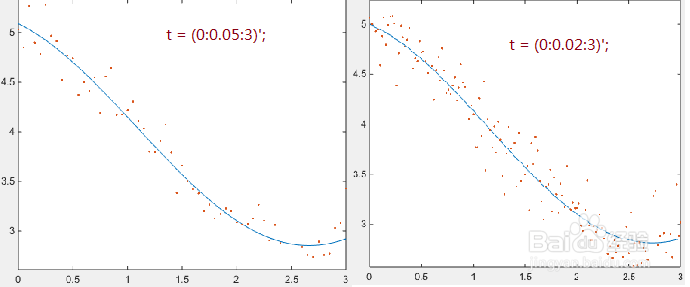
3、当改变取样点数量时,可以得到不同的结果。取样点越多,离实际值越接近。
4、 当函数形式是多项式时,最小二乘拟合过程由polyfit自动进行。 其他类型的拟合可以转换成为多项式形式。例如:y = ct^α可以变成logy = log c+α log t的形式,用于最常见线性拟合的图形数据拟合工具可从每个图窗口的“工具”菜单中获得。
5、如果拟合函数的未知系数呈现非线性,则会产生非线性优化。例如,MATLAB附带1790年至1990年的美国人口普查数据。 该数据每10年收集一次。 要使用c1 + c2*ec3^t形式的指数曲线拟合此数据,可以按以下步骤操作(需要优化工具箱支持):

6、 插值
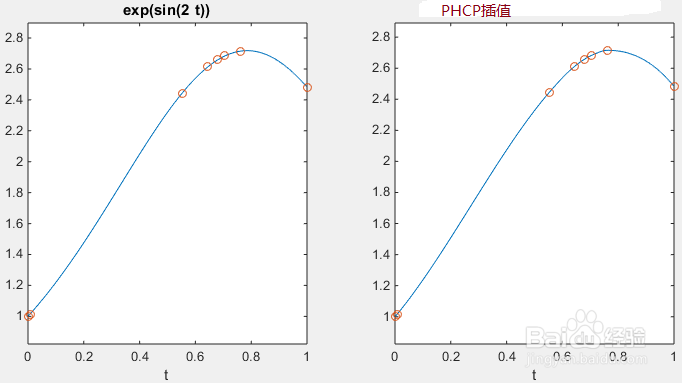
将离散值转换为连续变量的函数,但是这里函数无法被实际给定的数据约束。在一个变量中插值的主要函数是interp1。 例如,我们在6个随机点处对平滑函数进行采样,然后将分段三次插值多项式与原始多项式进行比较:

7、 调用interp1可以评估给定点处的插值多项式。 如果想创建一个可以计算的插值函数,可以使用不同形式的命令和匿名函数:interp1有几种不同类型的插值:‘nearest',产生分段常数阶梯近似;'linear',默认值,是分段线性的; 'spline',它是一个具有非结条件的分段三次样条;'pchip',它也是分段立方体,但牺牲了一些平滑度,以保持结果中的单调性和局部最大值和最小值。