1、第一步，点击键盘 win+r，打开运行窗口。在运行窗口中输入“cmd"，点击enter键，打开windows命令行窗口。
2、第二步，在windows命令行窗口中，输入“python”，点击enter键，进入python的命令交互窗口。
3、第三步，使用语句:“from sympy import *”，引入sympy模块的所有函数。
4、第四步，使用Function()创建符号函数变量g，使用Symbol()创建符号变量x。
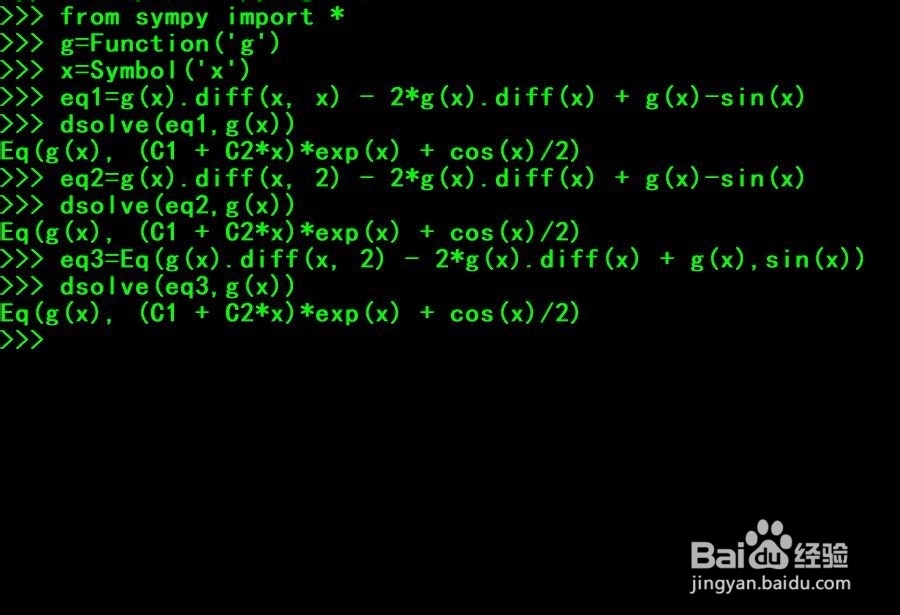
5、第五步，使用第一种方法，创建二阶微分方程g''(x)-2g'(x)+g(x)-sinx=0，并赋值该变量eq1。
6、第六步，使用函数dsolve(eq1,g(x))，求解二阶微分方程。
7、第七步，使用第二种方法创建二阶微分方程eq2，与第一种方法相比使用g(x).diff(x,2)表示二阶微分。同样使用函数dsolve(eq2,g(x))，求解二阶微分方程。
8、第八步，使用第三种方法创建二阶微分方程eq3，这种方法使用了函数Eq()来创建二阶微分方程g''烫喇霰嘴(x)-2g'(x)+g(x)-sinx=0。同样使用函数dsolve(eq2,g(x))，求解二阶微分方程。
9、第九步，使用第一种方法创建四阶微分方程g''''(x)-2涯箨唁峦*g'''(x)+5*g''(x)=0，并赋值给变量髫潋啜缅eq4，同样使用函数dsolve(eq4,g(x))，求解四阶微分方程。
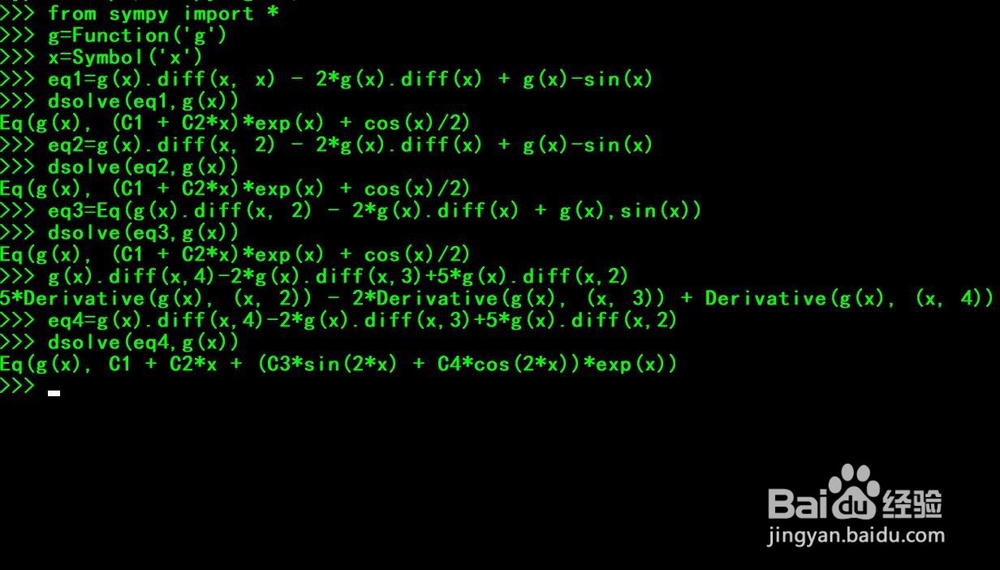
10、如果使用spyder编辑器，完整代码展示如下：
