1、根据函数y=lnx+√22x特征,对lnx有x>0,对于根式有x≥0,综合得x>0,即函数y=lnx+√22x的定义域为:(0,+∞)。

2、设A,B是两个非空的数集,如果按某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A--B为集合A到集合B的一个函数,记作y=f(x),x属于集合A。其中,x叫作自变量,x的取值范围A叫作函数的定义域。
3、计算函数y=lnx+√22x的导数,通过函数y=lnx+√22x一阶导数的符号,解析函数y=lnx+√22x的单调性,本题函数y=lnx+√22x为增函数。

4、解析函数y=lnx+√22x的凸凹性,计算函数的二阶导数,根据二阶导数的符号,因为小于0,所以函数y=lnx+√22x为凸函数。

5、如果一个函数f(x)在某个区间I上有f''(x)(即二阶导数)>0恒成立,那么在区间I上f(x)的图像上的任意两点连出的一条线段,这两点之间的函数图像都在该线段的下方,反之在该线段的上方。
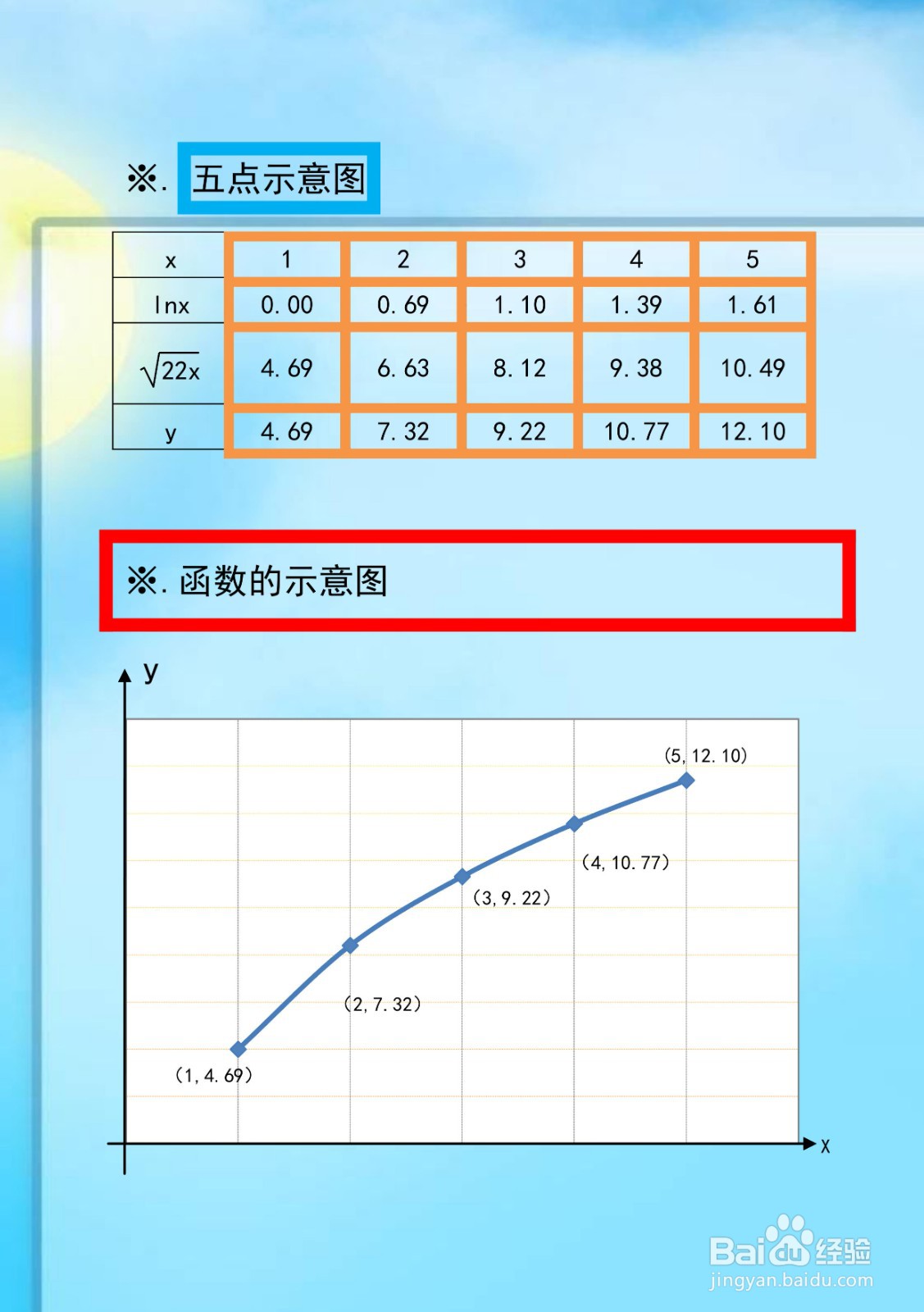
6、根据函数y=lnx+√22x的性质,解析函数上部分点图表,同时根据函数y=lnx+√22x的定义域、单调性及凸凹性等性质,即可简要画出函数y=lnx+√22x的图像示意图如下。